Công thức nguyên hàm lnx, các dạng bài tập và cách giải

Công thức nguyên hàm lnx, các dạng bài tập và cách giải

I. Lý thuyết

Để hiểu rõ hơn về công thức này, chúng ta cần biết rằng nguyên hàm của một hàm số f(x) là một hàm số F(x) mà đạo hàm của nó bằng hàm số f(x). Nguyên hàm của 1 hàm số f(x) thường được ký hiệu là ∫ ln(x).

Và trong trường hợp của hàm số ln(x), ta cần tìm một hàm số F(x) sao cho F'(x)=ln(x)dx. Hay nói các khác là:

∫ ln(x)dx = F(x) + C

Và ta có cách tính của nguyên hàm lnx là:

II. Cách tính nguyên hàm lnx

Cách 1: Sử dụng quy tắc tính nguyên hàm:

Theo quy tắc tính nguyên hàm, nguyên hàm của ln(x) là x * ln(x) - x + C, trong đó C là hằng số thuộc R.

Cách 2: Sử dụng phép tích phân:

Tích phân của lnx có thể tính bằng cách áp dụng phép tích phân không xác định như sau:

∫ ln(x) dx = x * ln(x) - ∫ x/x dx

Để tính ∫ x/x dx, chúng ta có thể đơn giản hóa bằng cách loại bỏ x/x:

∫ x/x dx = ∫ 1 dx

Suy ra, ta có:

∫ ln(x) dx = x * ln(x) - ∫ 1 dx

∫ ln(x) dx = x * ln(x) - x + C

III. Bài tập vận dụng

Bài tập 1: Tìm nguyên hàm của hàm số sau: ∫ x.lnx.dx

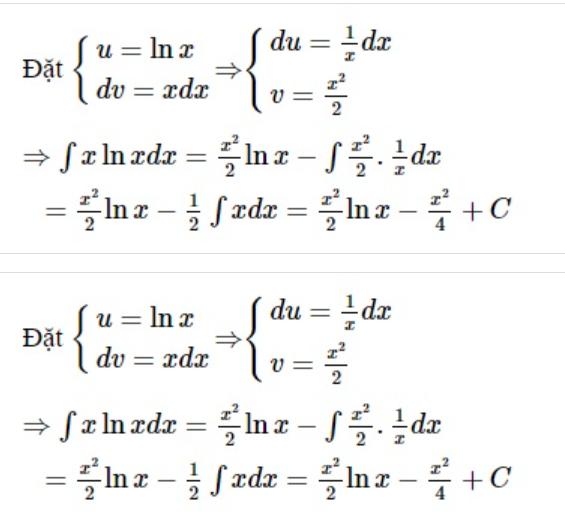
Bài tập 2: Với 12 ∫ln(x + 1)dx = aln3 + bln2 + c, trong đó a, b, c là các số nguyên. Tính S = a + b = c

Gợi ý lời giải:

Đặt u = ln(x + 1), dv = dx

=> du = 1/ (x + 1) dx, v = x + 1

Lúc này ta có:

Vậy ta có: a=3, b=-2, c=-1.

Từ đó suy ra => a+b+c=0

Bài tập 3: ∫ 2x.lnx(x - 1)dx

Gợi ý lời giải:

Đặt u= ln(x - 1), dv = 2x.dx

=> du = 1/(x - 1)dx, v =x2 - 1

Ta có: ∫ 2x.lnx(x - 1)dx

⇔ (x2 -1)ln(x -1) - ∫ (x + 1)

⇔ (x2 -1)ln(x -1) - ∫ (x + 1)

⇔ (x2 -1)ln(x -1) - (x2/2) - x + C

Đặt u = ln(1 +x), dv = (1/x2)dt

=>du= 1/(1+ x)dx, v = -1/x -1 = -(1+ x)/x

Từ đó suy ra: F(x) = -(1+ x)/x. ln(1 +x) + ∫(1/x)dx

= -(1+ x)/x. ln(1 +x) +lnx + C